1.ESTADISTICA

La estadística es una ciencia formal que estudia la recolección, análisis e interpretación de datos, ya sea para ayudar en la toma de decisiones o para explicar condiciones regulares o irregulares de algún fenómeno o estudio aplicado, de ocurrencia en forma aleatoria o condicional. Sin embargo estadística es más que eso, en otras palabras es el vehículo que permite llevar a cabo el proceso relacionado con la investigación científica.

                                         

1.1.     CONJUNTOS Y TECNICAS DE CONTEO

Si el número de posibles resultados de un experimento es pequeño, es relativamente fácil listar y contar todos los posibles resultados. Al tirar un dado, por ejemplo, hay seis posibles resultados.

Si, sin embargo, hay un gran número de posibles resultados tales como el número de niños y niñas por familias con cinco hijos, sería tedioso listar y contar todas las posibilidades.

Las posibilidades serían, 5 niños, 4 niños y 1 niña, 3 niños y 2 niñas, 2 niños y 3 niñas, etc. Para facilitar el conteo examinaremos tres técnicas: La técnica de la multiplicación, la técnica de la permutación, y la técnica de la combinación.

                                     

ü  la técnica de la multiplicación

La técnica de la multiplicación: Si hay m formas de hacer una cosa y hay n formas de hacer otra cosa, hay m x n formas da hacer ambas cosas

En términos de fórmula

Número total de arreglos = m x n

Esto puede ser extendido a más de dos eventos. Para tres eventos, m, n, y o:

Número total de arreglos = m x n x o

ü  La Técnica de la Permutación

Como vimos anteriormente la técnica de la multiplicación es aplicada para encontrar el número posible de arreglos para dos o más grupos. La técnica de la permutación es aplicada para encontrar el número posible de arreglos donde hay solo u grupo de objetos. Como ilustración analizaremos el siguiente problema: Tres componentes electrónicos - un transistor, un capacitor, y un diodo - serán ensamblados en una tablilla de una televisión. Los componentes pueden ser ensamblados en cualquier orden. ¿De cuantas diferentes maneras pueden ser ensamblados los tres componentes?

Las diferentes maneras de ensamblar los componentes son llamadas permutaciones, y son las siguientes:

T D C D T C C D T

T C D D C T C T D

Permutación: Todos los arreglos de r objetos seleccionados de n objetos posibles

La fórmula empleada para contar el número total de diferentes permutaciones es:

n P r = n!

            (n – r )!

Donde:

nPr es el número de permutaciones posible

n es el número total de objetos

r es el número de objetos utilizados en un mismo momento

n P r = n! = 3! = 3 x 2 = 6

     (n – r )!                 ( 3 – 3 )!                1

ü  La Técnica de la Combinación

En una permutación, el orden de los objetos de cada posible resultado es diferente. Si el orden de los objetos no es importante, cada uno de estos resultados se denomina combinación. Por ejemplo, si se quiere formar un equipo de trabajo formado por 2 personas seleccionadas de un grupo de tres (A, B y C). Si en el equipo hay dos funciones diferentes, entonces si importa el orden, los resultados serán permutaciones. Por el contrario si en el equipo no hay funciones definidas, entonces no importa el orden y los resultados serán combinaciones. Los resultados en ambos casos son los siguientes:

Permutaciones: AB, AC, BA, CA, BC, CB

Combinaciones: AB, AC, BC

Combinaciones: Es el número de formas de seleccionar r objetos de un grupo de n objetos sin importar el orden.

La fórmula de combinaciones es:

n C r = n!

r! (n – r )!

                                                  

1.1.2. DEFINICION Y NOTACION DE CONJUNTOS

Un conjunto es una colección bien definida de objetos a los cuales también llamamos los elementos de un conjunto.

A los conjuntos los identificamos con letras mayúsculas y a los elementos con letras minúsculas, encerrados en {}.

Los conjuntos se pueden describir de 2 formas:

1.- método de la lista. Consiste en enumerar a todos los elementos que pertenecen a dicho conjunto. Ejemplo:

         A= {1, 2, 3, 4, 5, 6}

         B= {a, e, i, o, u}

2.- método de la regla consiste en definir la característica común para ser considerado un elemento.

Ejemplo.

       A= x

      b= {x|x sea una letra vocal

Notación conjunto es una manera de decir cuál está en un conjunto. El conjunto se nombra generalmente con una mayúscula como esto:

A = {definición del conjunto}₁

La definición del conjunto está dentro de las llaves: {}. Hay dos estilos de la definición del conjunto que pueden estar en llaves.

• Lista: Si un conjunto tiene apenas algunos elementos, el conjunto puede ser definido enumerando todos los elementos:

B = {libro, lápiz, borrador}₂

En esta definición, el conjunto B tiene tres elementos: libro, lápiz, y borrador.

• Regla: Un conjunto se puede definir por una regla. Mientras que esta regla puede simplemente ser una oración por ejemplo {El conjunto de toda la roca en mi jardín.}, los símbolos de la matemáticas se utilizan típicamente:

C = {x | x ∈ ℕ, x < 20}₃

Conjunto C contiene todos los números naturales menos de 20

                                   

1.1.3. OPERACIONES Y LEYES DE CONJUNTOS

Si 1 designa al conjunto universal y 0 al conjunto vacío, las siguientes identidades son válidas en el álgebra de conjuntos para conjuntos arbitrarios X, Y, Z.

                                         

ü  Leyes conmutativas

XY = YX               X + Y = Y + X.

ü  Leyes asociativas

X (YZ) = (XY) Z               X + (Y + Z) = (X + Y) + Z.

ü  Leyes distributivas

X (Y + Z) = XY + XZ               X + YZ = (X + Y) (X + Z).

ü  Leyes de impotencia

XX = X               X + X = X.

ü  Leyes de complementación

XX' = 0               X + X' = 1.

ü  Leyes de absorción

X (X + Y) = X               X + XY = X.

ü  Leyes de Demoran

(XY)' = (X' + Y')               (X + Y )' = X'Y'.

ü  Leyes con 0 y 1

X 1 = X               X + 0 = X.
X 0 = 0               X + 1 = 1.
0' = 1               1' = 0.

ü  Ley de complemento doble

(X')' = X.

1.1.4. DIAGRAMA DE VEEN EULER

Los diagramas de Venn son ilustraciones usadas en la rama de la Matemática y Lógica de clase conocida como teoría de conjunto. Estos diagramas se usan para mostrar gráficamente la agrupación de cosas elementos en conjunto, representando cada conjunto mediante un círculo o un óvalo. La posición relativa en el plano de tales círculos muestra la relación entre los conjuntos. Por ejemplo, si los círculos de los conjuntos A y B se solapan, se muestra un área común a ambos conjuntos que contiene todos los elementos contenidos a la vez en A y en B. Si el círculo del conjunto A aparece dentro del círculo de otro B, es que todos los

elementos de A también están contenidos en B.

                                

                                                                       

1.1.5. PRINCIPIO ADITIVO Y MULTIPLICATIVO

PRINCIPIO ADITIVO: Si se desea llevar a efecto una actividad, la cuál tiene formas alternativas para ser realizada, donde la primera de esas alternativas puede ser realizada de M maneras o formas, la segunda alternativa puede realizarse de N maneras o formas ….. y la última de las alternativas puede ser realizada de W maneras o formas, entonces esa actividad puede ser llevada a cabo de,

             M + N +………+ W  maneras o formas

PRINCIPIO MULTIPLICATIVO: Si se desea realizar una actividad que consta de r pasos, en donde el primer paso de la actividad a realizar puede ser llevado a cabo de N1 maneras o formas, el segundo paso de N2 maneras o formas y el r-ésimo paso de Nr maneras o formas, entonces esta actividad puede ser llevada a efecto de;

                                     N1 x N2 x……….x  Nr  maneras o formas

El principio multiplicativo implica que cada uno de los pasos de la actividad debe ser llevado a efecto, uno tras otro.

1.1.6. DIAGRAMA DE ARBOL

Un diagrama de árbol es una herramienta que se utiliza para determinar todos los posibles resultados de un experimento aleatorio. En el cálculo de la probabilidad se requiere conocer el número de objetos que forman parte del espacio muestra, estos se pueden determinar con la construcción de un diagrama de árbol.

El diagrama de árbol es una representación gráfica de los posibles resultados del experimento, el cual consta una serie de pasos, donde cada uno de los pasos tiene un número finito de maneras de ser llevado a cabo. Se utiliza en los problemas de conteo y probabilidad.

                                         

1.1.7. PERNOCTACIONES

Es contar el número de eventos que cumplen con algún conjunto de condiciones. Sirve para calcular la probabilidad de un evento cuando el número de eventos posibles es muy grande.

1.1.8 COMBINACIONES

Como ya se menciono anteriormente, una combinación, es un arreglo de elementos en donde no nos interesa el lugar o posición que ocupan los mismos dentro del arreglo. En una combinación nos interesa formar grupos y el contenido de los mismos.

                                                

PARAMETROS

ESTIMACIÓN DE PARÁMETROS

INTRODUCCIÓN

El propósito de un estudio estadístico suele ser, como hemos venido citando, extraer conclusiones acerca de la naturaleza de una población. Al ser la población grande y no poder ser estudiada en su integridad en la mayoría de los casos, las conclusiones obtenidas deben basarse en el examen de solamente una parte de ésta, lo que nos lleva, en primer lugar a la justificación, necesidad y definición de las diferentes técnicas de muestreo.

Los primeros términos obligados a los que debemos hacer referencia serán los de estadístico y estimador.

Dentro de este contexto, será necesario asumir un estadístico o estimador como una variable aleatoria con una determinada distribución, y que será la pieza clave en las dos amplias categorías de la inferencia estadística: la estimación y el contraste de hipótesis.

El concepto de estimador, como herramienta fundamental, lo caracterizamos mediante una serie de propiedades que nos servirán para elegir el ``mejor" para un determinado parámetro de una población, así como algunos métodos para la obtención de ellos, tanto en la estimación puntual como por intervalos.

MUESTREO ALEATORIO

Consideremos una población finita, de la que deseamos extraer una muestra. Cuando el proceso de extracción es tal que garantiza a cada uno de los elementos de la población la misma oportunidad de ser incluidos en dicha muestra, denominamos al proceso de selección muestreo aleatorio. El muestreo aleatorio se puede plantear bajo dos puntos de vista: ·         Sin reposición de los elementos

·         Con reposición

ALEATORIO SIMPLE

Una muestra aleatoria simple es seleccionada de tal manera que cada muestra posible del mismo tamaño tiene igual probabilidad de ser seleccionada de la población. Para obtener una muestra aleatoria simple, cada elemento en la población tenga la misma probabilidad de ser seleccionado, el plan de muestreo puede no conducir a una muestra aleatoria simple. Por conveniencia, este método pude ser reemplazado por una tabla de números aleatorios. Cuando una población es infinita, es obvio que la tarea de numerar cada elemento de la población es infinita, es obvio que la tarea de numerar cada elemento de la población es imposible. Por lo tanto, ciertas modificaciones del muestreo aleatorio simple son necesarias. Los tipos más comunes de muestreo aleatorio modificado son sistemáticos, estratificados y de conglomerados.

                                                               

ESTRATIFICADO

. La estratificación tiene como objetivo principal aumentar la precisión global de la estimación sin incrementar el tamaño muestral.

Estratificar una población consiste en dividirla, “antes” de la extracción de la muestra, en subconjuntos homogéneos (respecto de caracteres determinados a priori), llamados estratos.

Los estratos deberán ser homogéneos en sí y heterogéneos entre sí respecto de la característica en estudio. La selección de la muestra se efectúa de manera independiente en el interior de cada estrato. Esto conlleva a que la varianza en cada estrato sea pequeña. Se trata de que los estratos sean lo más homogéneos posibles dentro de cada uno de ellos, es decir, que exista en cada uno la menor variabilidad posible y de que haya grandes diferencias de unos a otros estratos.

En lugar de extraer la muestra totalmente al azar, se extrae parte de la muestra en cada estrato

POR CONJUNTOS O MÉTODOS

El conjunto de Mandelbrot M se define como el conjunto de parámetros cC para los que el conjunto de Julia asociado a f_c=z²+c es conexo.

Esta definición no es adecuada para computar imágenes del conjunto de Mandelbrot. Para este fin es mucho más útil la caracterización dada por el siguiente teorema.

Teorema. M coincide con el conjunto de parámetros del plano complejo para los que la órbita (f_c^k(0)) está acotada. Esto equivale a que f_c^k(0) no tiende a infinito.

Como consecuencia del Teorema anterior se obtiene que M se encuentra acotado de la siguiente manera:

1. M está contenido en la bola de radio 2 (puesto que c=-2 está en M, esta acotación es óptima),
2. M intersección con R es el intervalo [-2,1/4].

EN DOS ETAPAS

NO NECESARIAMENTE IGUALES

 

                                                    

DATOS APAREADOS

Los datos apareados son los que tenemos cuando dos muestras con valores pero los datos de cada muestra pertenecen a los mismos individuos, es decir tenemos las medidas de cada variable en la misma persona o individuo, por ejemplo medimos los valores de tensión arterial mínimo y máximo, si sacamos la muestra en el mismo grupo de personas, para cada una de ellas dispondremos de dos valores uno para cada muestra, que están relacionados (apareados) al ser del mismo individuo, por ejemplo hemos medido la tensión máxima y mínima en las 4 personas.

Persona --- mínimo --- máximo
1 --- 110 --- 135
2 --- 90 --- 115
3 --- 101 --- 121
4 ---- 120 --- 150

Es diferente a  haber medido la tensión máxima en 4 persona y la mínima en otras 4.

Los datos apareados pueden usarse fácilmente en varias pruebas estadísticas ya que basta crear una variable que mida su diferencia en cada individuo y trabajar con una sola variable en lugar de dos.

PRUEBA DE HIPÓTESIS

INTRODUCCIÓN

Referente al contraste de hipótesis, sabemos que un problema es investigable cuando existen dos o más soluciones alternativas y tenemos dudas acerca de cuál de ellas es la mejor. Esta situación permite formular una o más hipótesis de trabajo, ya que cada una de ellas destaca la conveniencia de una de las soluciones sobre las demás. Si nuestro propósito es comprobar una teoría ella misma será la hipótesis del trabajo, pero es importante destacar que al formular dicha o dichas hipótesis no significa que ya esté resuelto el problema, al contrario, que nuestra duda nos impulsa a comprobar la verdad o falsedad de cada una de ellas.

La decisión final partirá de las decisiones previas de aceptar o rechazar las hipótesis de trabajo.

DEFINICIÓN DE HIPÓTESIS

La hipótesis tiene como propósito llegar a la comprensión del porqué entre dos elementos se establece algún tipo definido de relación y establece que la hipótesis:

"Es una proposición respecto a alguno elementos empíricos y otros conceptos y sus relaciones mutuas, que emerge mas allá de los hechos y las experiencias conocidas, con el propósito de llegar a una mayor comprensión de los mismos".

FUENTES DE HIPÓTESIS

Al realizar pruebas de hipótesis, se parte de un valor supuesto (hipotético) en parámetro poblacional. Después de recolectar una muestra aleatoria, se compara la estadística muestral, así como la media (x), con el parámetro hipotético, se compara con una supuesta media poblacional (m). Después se acepta o se rechaza el valor hipotético, según proceda. Se rechaza el valor hipotético sólo si el resultado muestral resulta muy poco probable cuando la hipótesis es cierta.

HIPÓTESIS NULA Y ALTERNATIVA

Hipótesis Nula:

En muchos casos formulamos una hipótesis estadística con el único propósito de rechazarla o invalidarla. Así, si queremos decidir si una moneda está trucada, formulamos la hipótesis de que la moneda es buena (o sea p = 0,5, donde p es la probabilidad de cara).

Analógicamente, si deseamos decidir si un procedimiento es mejor que otro, formulamos la hipótesis de que no hay diferencia entre ellos (o sea. Que cualquier diferencia observada se debe simplemente a fluctuaciones en el muestreo de la misma población). Tales hipótesis se suelen llamar hipótesis nula y se denotan por H₀.

Hipótesis Alternativa.

Toda hipótesis que difiere de una dada se llamará una hipótesis alternativa. Por ejemplo: Si una hipótesis es p = 0,5, hipótesis alternativa podrían ser p = 0,7, p ¹ 0,5 ó p > 0,5.

Una hipótesis alternativa a la hipótesis nula se denotará por H₁.

1.- Planear la hipótesis nula y la hipótesis alternativa. La hipótesis nula (H₀) es el valor hipotético del parámetro que se compra con el resultado muestral resulta muy poco probable cuando la hipótesis es cierta

Consecuencias de las Decisiones en Pruebas de Hipótesis.

Decisiones Posibles	Situaciones Posibles
	La hipótesis nula es verdadera	La hipótesis nula es falsa
Aceptar la Hipótesis Nula	Se acepta correctamente	Error tipo II
Rechazar la Hipótesis Nula	Error tipo I	Se rechaza correctamente

HIPÓTESIS SIMPLES Y COMPUESTAS

• Hipótesis simple: Aquella en la que se especifica un único valor del parámetro. Este es el caso de las hipótesis nulas en los dos últimos contrastes mencionados.

• Hipótesis compuesta: Aquella en la que se especifica más de un posible valor del parámetro. Por ejemplo tenemos que son compuestas las hipótesis alternativas de esos mismos contrastes.

PRUEBAS BILATERALES Y UNILATERALES

 

ERRORES TIPO I Y II

Errores de tipo I

Si rechazamos una hipótesis cuando debiera ser aceptada, diremos que se ha cometido un error de tipo I.

Por otra parte, si aceptamos una hipótesis que debiera ser rechazada, diremos que se cometió un

Error de tipo II.

En ambos casos, se ha producido un juicio erróneo.

Para que las reglas de decisión (o no contraste de hipótesis) sean buenos, deben diseñarse de modo que minimicen los errores de la decisión; y no es una cuestión sencilla, porque para cualquier tamaño de la muestra, un intento de disminuir un tipo de error suele ir acompañado de un crecimiento del otro tipo. En la práctica, un tipo de error puede ser más grave que el otro, y debe alcanzarse un compromiso que disminuya el error más grave.

La única forma de disminuir ambos a la vez es aumentar el tamaño de la muestra que no siempre es posible.

MATRIZ DE DECISIÓN

                                                    

ESTIMACIÓN PUNTUAL

La estimación por intervalos de confianza tiene por objeto proporcionar, a partir de la información recogida en la muestra, un intervalo que contenga con alto nivel de confianza (probabilidad), al parámetro objeto de nuestro interés. A partir de dicho intervalo obtendremos una medida del error máximo cometido al aproximar puntualmente el parámetro.

MÉTODOS

Es   una proposición aceptable que ha sido formulada a través de la recolección de información y datos, aunque no está confirmada sirve para responder de forma tentativa a un problema con base científica.
Con base en lo que nos dice la definición que acabamos de presentar podemos decir que la hipótesis puede usarse como una propuesta provisional que no pretende demostrar estrictamente la solución de un problema o situación pero que se basa de argumentos firmes.
El nivel de veracidad que se le otorga a una hipótesis depende de la medida en que los datos empíricos apoyan lo que se está afirmando. Esto es lo que se conoce como contrastación empírica de la hipótesis esto también lo podemos llamar como proceso de validación de la hipótesis.

                                                   

                                                        

MÁXIMA VEROSIMILITUD

                                                                 

MOMENTOS

Etapa 1.- Planear la hipótesis nula y la hipótesis alternativa. La hipótesis nula (H0) es el valor hipotético del parámetro que se compra con el resultado muestral resulta muy poco probable cuando la hipótesis es cierta.

Etapa 2.- Especificar el nivel de significancia que se va a utilizar. El nivel de significancia del 5%, entonces se rechaza la hipótesis nula solamente si el resultado muestral es tan diferente del valor hipotético que una diferencia de esa magnitud o mayor, pudiera ocurrir aleatoria mente con una probabilidad de 1.05 o menos.

Etapa 3.- Elegir la estadística de prueba. La estadística de prueba puede ser la estadística muestral (el estimador no segado del parámetro que se prueba) o una versión transformada de esa estadística muestral. Por ejemplo, para probar el valor hipotético de una media poblacional, se toma la media de una muestra aleatoria de esa distribución normal, entonces es común que se transforme la media en un valor z el cual, a su vez, sirve como estadística de prueba.

Etapa 4.- Establecer el valor o valores críticos de la estadística de prueba. Habiendo especificado la hipótesis nula, el nivel de significancia y la estadística de prueba que se van a utilizar, se produce a establecer el o los valores críticos de estadística de prueba. Puede haber uno o más de esos valores, dependiendo de si se va a realizar una prueba de uno o dos extremos.

Etapa 5.- Determinar el valor real de la estadística de prueba. Por ejemplo, al probar un valor hipotético de la media poblacional, se toma una muestra aleatoria y se determina el valor de la media muestral. Si el valor crítico que se establece es un valor de z, entonces se transforma la media muestral en un valor de z.

Etapa 6.- Tomar la decisión. Se compara el valor observado de la estadística muestral con el valor (o valores) críticos de la estadística de prueba. Después se acepta o se rechaza la hipótesis nula. Si se rechaza ésta, se acepta la alternativa; a su vez, esta decisión tendrá efecto sobre otras decisiones de los administradores operativos, como por ejemplo, mantener o no un estándar de desempeño o cuál de dos estrategias de mercadotecnia utilizar.

INSESGADO DE VARIANZA. MÍNIMA

                                                     

ESTIMACIÓN POR INTERVALOS DE CONFIANZA

Las líneas verticales representan 50 construcciones diferentes de intervalos de confianza para la estimación del valor μ.

En estadística, se llama intervalo de confianza a un par de números entre los cuales se estima que estará cierto valor desconocido con una determinada probabilidad de acierto. Formalmente, estos números determinan un intervalo, que se calcula a partir de datos de una muestra, y el valor desconocido es un parámetro poblacional. La probabilidad de éxito en la estimación se representa con 1 - α y se denomina nivel de confianza. En estas circunstancias, α es el llamado error aleatorio o nivel de significación, esto es, una medida de las posibilidades de fallar en la estimación mediante tal intervalo.^[1]

El nivel de confianza y la amplitud del intervalo varían conjuntamente, de forma que un intervalo más amplio tendrá más posibilidades de acierto (mayor nivel de confianza), mientras que para un intervalo más pequeño, que ofrece una estimación más precisa, aumentan sus posibilidades de error.

Para la construcción de un determinado intervalo de confianza es necesario conocer la distribución teórica que sigue el parámetro a estimar, θ. Es habitual que el parámetro presente una distribución normal. También pueden construirse intervalos de confianza con la desigualdad de Chebyshov.

En definitiva, un intervalo de confianza al 1 - α por ciento para la estimación de un parámetro poblacional θ que sigue una determinada distribución de probabilidad, es una expresión del tipo [θ₁, θ₂] tal que P[θ₁ ≤ θ ≤ θ₂] = 1 - α, donde P es la función de distribución de probabilidad de θ.

DE LA DESVIACIÓN ESTÁNDAR

La desviación estándar o desviación típica (denotada con el símbolo σ o s, dependiendo de la procedencia del conjunto de datos) es una medida de centralización o dispersión para variables de razón (ratio o cociente) y de intervalo, de gran utilidad en la estadística descriptiva.

Se define como la raíz cuadrada de la varianza. Junto con este valor, la desviación típica es una medida (cuadrática) que informa de la media de distancias que tienen los datos respecto de su media aritmética, expresada en las mismas unidades que la variable.

Para conocer con detalle un conjunto de datos, no basta con conocer las medidas de tendencia central, sino que necesitamos conocer también la desviación que presentan los datos en su distribución respecto de la media aritmética de dicha distribución, con objeto de tener una visión de los mismos más acorde con la realidad al momento de describirlos e interpretarlos para la toma de decisiones

DE LA DIFERENCIA DE MEDIDAS CON A¨S CONOCIDAS

En esta sección se verá el caso en donde se tienen dos poblaciones con medias y varianzas desconocidas, y se desea encontrar un intervalo de confianza para la diferencia de dos medias _ _Si los tamaños de muestras n₁ y n₂ son mayores que 30, entonces, puede emplearse el intervalo de confianza de la distribución normal. Sin embargo, cuando se toman muestras pequeñas se supone que las poblaciones de interés están distribuidas de manera normal, y los intervalos de confianza se basan en la distribución t.

  

PROCEDIMIENTO DE PRUEBA DE HIPÓTESIS

PRUEBA DE HIPOTESIS: Procedimiento basado en la evidencia muestral y en la teoría de probabilidad que se emplea para determinar si la hipótesis es un enunciado razonable y no debe rechazarse o si es ir racionable y debe ser rechazada.

PROCEDIMIENTO DE 5 PASOS PARA PROBAR UNA HIPOTESIS

PASO 1.- PLANTEAMIENTO DE HIPOTESIS.

- Ho: Hipótesis Nula

- H1: Hipótesis Alternativo

• Hipótesis Nula.- Una afirmación o enunciado tentativo que se realiza acerca del valor de un parámetro poblacional. Por lo común en una afirmación de que el parámetro de población tiene valor especifico.
• Hipótesis Alternativa.- Una afirmación o enunciado que se aceptara si los datos muéstrales proporcionan amplia evidencia de que la hipótesis nula es falsa

PASO 2.- NIVELES DE SIGNIFICACION.

El riesgo que se asume acerca e rechazar la hipótesis nula cuando en realidad deben asemejarse por ser verdadera. El nivel de significación se denota mediante la letra griega sigma.

No hay un nivel de significación que se aplique a todos los estudios que implican muestreo. Deben tomarse una decisión de usar el nivel 0.05, el nivel 0.01, el 0.10 o cualquier otro nivel entre 0 y 1

Tradicionalmente se relaciona el nivel 0.05 para proyectos de investigación sobre consumo, el 0.01 para control de calidad y el 0.10 para encuesta políticas. Como investigador debe decidir el nivel de significación antes de formular una regla de decisión y recopilar datos muestrales.

ERROR TIPO 1.- La probabilidad de rechazar la hipótesis nula cuando en realidad es verdadera.

ERROR TIPO 2.- L probabilidad de aceptar la hipótesis nula cuando en realidad es falsa.

PASO 3.- ESTADISTICO DE PRUEBA

Un valor, determinado a partir de la información muestral, que se utiliza para aceptar o rechazar la hipótesis nula.

PASO 4.- REGLA DE DECISION

Es una regla simple la cual es una afirmación de las condiciones bajo las que se acepta la hipótesis nula.

PASO 5.- TOMA DE DECISION

Es la toma de decisión si se debe aceptar o rechazar la hipótesis nula.

PROCEDIMIENTO DE PRUEBA DE HIPÓTESIS

Paso 1:

 Plantear la hipótesis nula Ho y la hipótesis alternativa H1.

Cualquier investigación estadística implica la existencia de hipótesis o afirmaciones acerca de las poblaciones que se estudian.

La hipótesis nula (Ho) se refiere siempre a un valor especificado del parámetro de población, no a una estadística de muestra. La letra H significa hipótesis y el subíndice cero no hay diferencia. Por lo general hay un "no" en la hipótesis nula que indica que "no hay cambio" Podemos rechazar o aceptar Ho.

La hipótesis nula es una afirmación que no se rechaza a menos que los datos maestrales proporcionen evidencia convincente de que es falsa. El planteamiento de la hipótesis nula siempre contiene un signo de igualdad con respecto al valor especificado del parámetro.

La hipótesis alternativa (H1) es cualquier hipótesis que difiera de la hipótesis nula. Es una afirmación que se acepta si los datos maestrales proporcionan evidencia suficiente de que la hipótesis nula es falsa. Se le conoce también como la hipótesis de investigación. El planteamiento de la hipótesis alternativa nunca contiene un signo de igualdad con respecto al valor especificado del parámetro.

Paso 2:

Seleccionar el nivel de significancia.

Nivel de significacia: Probabilidad de rechazar la hipótesis nula cuando es verdadera. Se le denota mediante la letra griega α, tambiιn es denominada como nivel de riesgo, este termino es mas adecuado ya que se corre el riesgo de rechazar la hipótesis nula, cuando en realidad es verdadera. Este nivel esta bajo el control de la persona que realiza la prueba.

Si suponemos que la hipótesis planteada es verdadera, entonces, el nivel de significación indicará la probabilidad de no aceptarla, es decir, estén fuera de área de aceptación. El nivel de confianza (1-α), indica la probabilidad de aceptar la hipótesis planteada, cuando es verdadera en la poblacion

                                                  

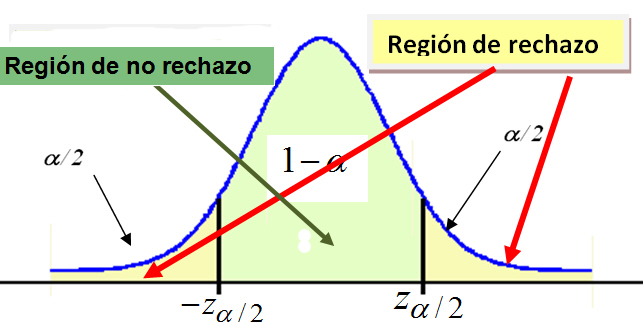
La distribución de muestreo de la estadística de prueba se divide en dos regiones, una región de rechazo (conocida como región crítica) y una región de no rechazo (aceptación). Si la estadística de prueba cae dentro de la región de aceptación, no se puede rechazar la hipótesis nula.

La región de rechazo puede considerarse como el conjunto de valores de la estadística de prueba que no tienen posibilidad de presentarse si la hipótesis nula es verdadera. Por otro lado, estos valores no son tan improbables de presentarse si la hipótesis nula es falsa. El valor crítico separa la región de no rechazo de la de rechazo.

PARÁMETROS

En estadística, un parámetro es un número que resume la ingente cantidad de datos que pueden derivarse del estudio de una variable estadística. El cálculo de este número está bien definido, usualmente mediante una fórmula aritmética obtenida a partir de datos de la población

Los parámetros estadísticos son una consecuencia inevitable del propósito esencial de la estadística: crear un modelo de la realidad.

El estudio de una gran cantidad de datos individuales de una población puede ser farragoso e inoperativo, por lo que se hace necesario realizar un resumen que permita tener una idea global de la población, compararla con otras, comprobar su ajuste a un modelo ideal, realizar estimaciones sobre datos desconocidos de la misma y, en definitiva, tomar decisiones. A estas tareas contribuyen de modo esencial los parámetros estadísticos.

Por ejemplo, suele ofrecerse como resumen de la juventud de una población la media aritmética de las edades de sus miembros, esto es, la suma de todas ellas, dividida por el total de individuos que componen tal población.

PRUEBAS PARAMÉTRICAS

PRUEBAS NO PARAMÉTRICAS

La estadística no paramétrica es una rama de la estadística que estudia las pruebas y modelos estadísticos cuya distribución subyacente no se ajusta a los llamados criterios paramétricos. Su distribución no puede ser definida a prioriodo, pues son los datos observados los que la determinan. La utilización de estos métodos se hace recomendable cuando no se puede asumir que los datos se ajusten a una distribución conocida, cuando el nivel de medida empleado no sea, como mínimo, de intervalo.

PRUEBA DE BONDAD DE AJUSTE

PRUEBA DE CHI-CUADRADA

Esta prueba puede utilizarse incluso con datos medibles en una escala nominal. La hipótesis nula de la prueba Chi-cuadrado postula una distribución de probabilidad totalmente especificada como el modelo matemático de la población que ha generado la muestra.

Para realizar este contraste se disponen los datos en una tabla de frecuencias. Para cada valor o intervalo de valores se indica la frecuencia absoluta observada o empírica (Oi). A continuación, y suponiendo que la hipótesis nula es cierta, se calculan para cada valor o intervalo de valores la frecuencia absoluta que cabría esperar o frecuencia esperada (Ei=n·pi , donde n es el tamaño de la muestra y pi la probabilidad del i-ésimo valor o intervalo de valores según la hipótesis nula). El estadístico de prueba se basa en las diferencias entre la Oi y Ei y se define como:

Este estadístico tiene una distribución Chi-cuadrado con k-1 grados de libertad si n es suficientemente grande, es decir, si todas las frecuencias esperadas son mayores que 5. En la práctica se tolera un máximo del 20% de frecuencias inferiores a 5.

Si existe concordancia perfecta entre las frecuencias observadas y las esperadas el estadístico tomará un valor igual a 0; por el contrario, si existe una gran discrepancias entre estas frecuencias el estadístico tomará un valor grande y, en consecuencia, se rechazará la hipótesis nula. Así pues, la región crítica estará situada en el extremo superior de la distribución Chi-cuadrado con k-1 grados de libertad.

Para realizar un contraste Chi-cuadrado la secuencia es:

Analizar

Pruebas no paramétricas

Chi-cuadrado

En el cuadro de diálogo Prueba chi-cuadrado se indica la variable a analizar en Contrastar variables.

En Valores esperados se debe especificar la distribución teórica activando una de las dos alternativas. Por defecto está activada Todas la categorías iguales que recoge la hipótesis de que la distribución de la población es uniforme discreta. La opción Valores requiere especificar uno a uno los valores esperados de las frecuencias relativas o absolutas correspondientes a cada categoría, introduciéndolos en el mismo orden en el que se han definido las categorías.

El recuadro Rango esperado presenta dos opciones: por defecto está activada Obtener de los datos que realiza el análisis para todas las categorías o valores de la variable; la otra alternativa, Usar rango especificado, realiza el análisis sólo para un determinado rango de valores cuyos límites Inferior y Superior se deben especificar en los recuadros de texto correspondientes.

El cuadro de diálogo al que se accede con el botón Opciones ofrece la posibilidad de calcular los Estadísticos Descriptivos y/o los Cuartiles, así como seleccionar la forma en que se desea tratar los valores perdidos.

PRUEBA DE KOLMOGOROV- SMIRNOFF