1.ESTADISTICA
La estadística es una ciencia formal que estudia la recolección, análisis e interpretación de datos, ya sea para ayudar en la toma de decisiones o para explicar condiciones regulares o irregulares de algún fenómeno o estudio aplicado, de ocurrencia en forma aleatoria o condicional. Sin embargo estadística es más que eso, en otras palabras es el vehículo que permite llevar a cabo el proceso relacionado con la investigación científica.
1.1. CONJUNTOS Y TECNICAS DE CONTEO
Si el número de posibles resultados de un experimento es pequeño, es relativamente fácil listar y contar todos los posibles resultados. Al tirar un dado, por ejemplo, hay seis posibles resultados.
Si, sin embargo, hay un gran número de posibles resultados tales como el número de niños y niñas por familias con cinco hijos, sería tedioso listar y contar todas las posibilidades.
Las posibilidades serían, 5 niños, 4 niños y 1 niña, 3 niños y 2 niñas, 2 niños y 3 niñas, etc. Para facilitar el conteo examinaremos tres técnicas: La técnica de la multiplicación, la técnica de la permutación, y la técnica de la combinación.
ü la técnica de la multiplicación
La técnica de la multiplicación: Si hay m formas de hacer una cosa y hay n formas de hacer otra cosa, hay m x n formas da hacer ambas cosas
En términos de fórmula
Número total de arreglos = m x n
Esto puede ser extendido a más de dos eventos. Para tres eventos, m, n, y o:
Número total de arreglos = m x n x o
ü La Técnica de la Permutación
Como vimos anteriormente la técnica de la multiplicación es aplicada para encontrar el número posible de arreglos para dos o más grupos. La técnica de la permutación es aplicada para encontrar el número posible de arreglos donde hay solo u grupo de objetos. Como ilustración analizaremos el siguiente problema: Tres componentes electrónicos - un transistor, un capacitor, y un diodo - serán ensamblados en una tablilla de una televisión. Los componentes pueden ser ensamblados en cualquier orden. ¿De cuantas diferentes maneras pueden ser ensamblados los tres componentes?
Las diferentes maneras de ensamblar los componentes son llamadas permutaciones, y son las siguientes:
T D C D T C C D T
T C D D C T C T D
Permutación: Todos los arreglos de r objetos seleccionados de n objetos posibles
La fórmula empleada para contar el número total de diferentes permutaciones es:
n P r = n!
(n – r )!
Donde:
nPr es el número de permutaciones posible
n es el número total de objetos
r es el número de objetos utilizados en un mismo momento
n P r = n! = 3! = 3 x 2 = 6
(n – r )! ( 3 – 3 )! 1
ü La Técnica de la Combinación
En una permutación, el orden de los objetos de cada posible resultado es diferente. Si el orden de los objetos no es importante, cada uno de estos resultados se denomina combinación. Por ejemplo, si se quiere formar un equipo de trabajo formado por 2 personas seleccionadas de un grupo de tres (A, B y C). Si en el equipo hay dos funciones diferentes, entonces si importa el orden, los resultados serán permutaciones. Por el contrario si en el equipo no hay funciones definidas, entonces no importa el orden y los resultados serán combinaciones. Los resultados en ambos casos son los siguientes:
Permutaciones: AB, AC, BA, CA, BC, CB
Combinaciones: AB, AC, BC
Combinaciones: Es el número de formas de seleccionar r objetos de un grupo de n objetos sin importar el orden.
La fórmula de combinaciones es:
n C r = n!
r! (n – r )!
1.1.2. DEFINICION Y NOTACION DE CONJUNTOS
Un conjunto es una colección bien definida de objetos a los cuales también llamamos los elementos de un conjunto.
A los conjuntos los identificamos con letras mayúsculas y a los elementos con letras minúsculas, encerrados en {}.
Los conjuntos se pueden describir de 2 formas:
1.- método de la lista. Consiste en enumerar a todos los elementos que pertenecen a dicho conjunto. Ejemplo:
A= {1, 2, 3, 4, 5, 6}
B= {a, e, i, o, u}
2.- método de la regla consiste en definir la característica común para ser considerado un elemento.
Ejemplo.
A= x
b= {x|x sea una letra vocal
Notación conjunto es una manera de decir cuál está en un conjunto. El conjunto se nombra generalmente con una mayúscula como esto:
A = {definición del conjunto}1
La definición del conjunto está dentro de las llaves: {}. Hay dos estilos de la definición del conjunto que pueden estar en llaves.
- Lista: Si un conjunto tiene apenas algunos elementos, el conjunto puede ser definido enumerando todos los elementos:
B = {libro, lápiz, borrador}2
En esta definición, el conjunto B tiene tres elementos: libro, lápiz, y borrador.
- Regla: Un conjunto se puede definir por una regla. Mientras que esta regla puede simplemente ser una oración por ejemplo {El conjunto de toda la roca en mi jardín.}, los símbolos de la matemáticas se utilizan típicamente:
C = {x | x ∈ ℕ, x < 20}3
Conjunto C contiene todos los números naturales menos de 20
1.1.3. OPERACIONES Y LEYES DE CONJUNTOS
Si 1 designa al conjunto universal y 0 al conjunto vacío, las siguientes identidades son válidas en el álgebra de conjuntos para conjuntos arbitrarios X, Y, Z.
ü Leyes conmutativas
XY = YX X + Y = Y + X.
ü Leyes asociativas
X (YZ) = (XY) Z X + (Y + Z) = (X + Y) + Z.
ü Leyes distributivas
X (Y + Z) = XY + XZ X + YZ = (X + Y) (X + Z).
ü Leyes de impotencia
XX = X X + X = X.
ü Leyes de complementación
XX' = 0 X + X' = 1.
ü Leyes de absorción
X (X + Y) = X X + XY = X.
ü Leyes de Demoran
(XY)' = (X' + Y') (X + Y )' = X'Y'.
ü Leyes con 0 y 1
X 1 = X X + 0 = X.
X 0 = 0 X + 1 = 1.
0' = 1 1' = 0.
X 0 = 0 X + 1 = 1.
0' = 1 1' = 0.
ü Ley de complemento doble
(X')' = X.
1.1.4. DIAGRAMA DE VEEN EULER
Los diagramas de Venn son ilustraciones usadas en la rama de la Matemática y Lógica de clase conocida como teoría de conjunto. Estos diagramas se usan para mostrar gráficamente la agrupación de cosas elementos en conjunto, representando cada conjunto mediante un círculo o un óvalo. La posición relativa en el plano de tales círculos muestra la relación entre los conjuntos. Por ejemplo, si los círculos de los conjuntos A y B se solapan, se muestra un área común a ambos conjuntos que contiene todos los elementos contenidos a la vez en A y en B. Si el círculo del conjunto A aparece dentro del círculo de otro B, es que todos los
elementos de A también están contenidos en B.
1.1.5. PRINCIPIO ADITIVO Y MULTIPLICATIVO
PRINCIPIO ADITIVO: Si se desea llevar a efecto una actividad, la cuál tiene formas alternativas para ser realizada, donde la primera de esas alternativas puede ser realizada de M maneras o formas, la segunda alternativa puede realizarse de N maneras o formas ….. y la última de las alternativas puede ser realizada de W maneras o formas, entonces esa actividad puede ser llevada a cabo de,
M + N +………+ W maneras o formas
PRINCIPIO MULTIPLICATIVO: Si se desea realizar una actividad que consta de r pasos, en donde el primer paso de la actividad a realizar puede ser llevado a cabo de N1 maneras o formas, el segundo paso de N2 maneras o formas y el r-ésimo paso de Nr maneras o formas, entonces esta actividad puede ser llevada a efecto de;
N1 x N2 x……….x Nr maneras o formas
El principio multiplicativo implica que cada uno de los pasos de la actividad debe ser llevado a efecto, uno tras otro.
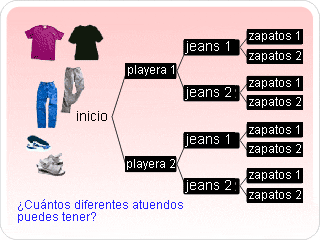
1.1.6. DIAGRAMA DE ARBOL
Un diagrama de árbol es una herramienta que se utiliza para determinar todos los posibles resultados de un experimento aleatorio. En el cálculo de la probabilidad se requiere conocer el número de objetos que forman parte del espacio muestra, estos se pueden determinar con la construcción de un diagrama de árbol.
El diagrama de árbol es una representación gráfica de los posibles resultados del experimento, el cual consta una serie de pasos, donde cada uno de los pasos tiene un número finito de maneras de ser llevado a cabo. Se utiliza en los problemas de conteo y probabilidad.

1.1.7. PERNOCTACIONES
Es contar el número de eventos que cumplen con algún conjunto de condiciones. Sirve para calcular la probabilidad de un evento cuando el número de eventos posibles es muy grande.
1.1.8 COMBINACIONES
Como ya se menciono anteriormente, una combinación, es un arreglo de elementos en donde no nos interesa el lugar o posición que ocupan los mismos dentro del arreglo. En una combinación nos interesa formar grupos y el contenido de los mismos.
No hay comentarios:
Publicar un comentario