TEORÍA DE LA PROBABILIDAD
ESPACIO MUESTRAL
EVENTOS

AXIOMA Y TEOREMAS DE LA PROBABILIDAD
AXIOMAS Y TEOREMAS
Para el cálculo de probabilidades hay que tomar en cuenta los Axiomas y Teoremas que a continuación se enumeran.
1)La probabilidad de que ocurra un evento A cualquiera se encuentra entre cero y uno.
0 £ p(A) ³ 1
2)La probabilidad de que ocurra el espacio muestral d debe de ser 1.
p(d) = 1
3)Si A y B son eventos mutuamente excluyentes, entonces la p(AÈB) = p(A) + p(B)
Generalizando:
Si se tienen n eventos mutuamente excluyentes o exclusivos A1, A2, A3,.....An, entonces;
p(A1ÈA2È.........ÈAn) = p(A1) + p(A2) + .......+ p(An)

PROBABILIDAD CONDICIONAL
PROBABILIDAD CONDICIONAL
PROBABILIDAD TOTAL Y TEOREMA DE BAYES
DISTRIBUCIONES
DISTRIBUCIÓN NORMAL
La gráfica de su función de densidad tiene una forma acampanada y es simétrica respecto de un determinado parámetro estadístico. Esta curva se conoce como campana de Gauss y es el gráfico de una función gaussiana.La importancia de esta distribución radica en que permite modelar numerosos fenómenos naturales, sociales y psicológicos. Mientras que los mecanismos que subyacen a gran parte de este tipo de fenómenos son desconocidos, por la enorme cantidad de variables incontrolables que en ellos intervienen, el uso del modelo normal puede justificarse asumiendo que cada observación se obtiene como la suma de unas pocas causas independientes

TEOREMA DE LA COMBINACIÓN LINEAL DE VARIACIONES NORMALES Y CHI-CUADRADAS
Terorema de Chebshev, este teorema da una estimación conservadora de la probabilidad de que una variable aleatoria tome un valor dentro de k dentro de k desviaciones estándar de su media para cualquier número real k. Proporcionaremos solo la demostración para caso continuo.La probabilidad de que cualquier variable aleatoria X tome un valor dentro de k desviaciones estándar de la media es al menos 1-
DISTRIBUCIONES MUÉSTRALES
En estadística, la distribución muestral es lo que resulta de considerar todas las muestras posibles que pueden ser tomadas de una población. Su estudio permite calcular la probabilidad que se tiene, dada una sola muestra, de acercarse al parámetro de la población. Mediante la distribución muestral se puede estimar el error para un tamaño de muestra dado.


DISTRIBUCIONES. NORMAL
DISTRIBUCIONES. T.

DISTRIBUCIONES. NORMAL DOS PARÁMETROS

DISTRIBUCIONES. T DOS PARÁMETROS
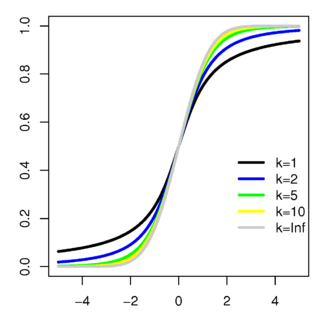
DISTRIBUCIONES. F.

No hay comentarios:
Publicar un comentario